Diffusion Models for Time Series Analysis
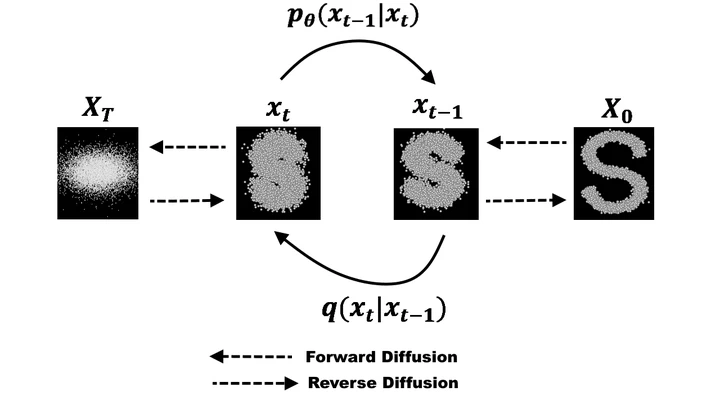 A visual representation of a Diffusion Model
A visual representation of a Diffusion ModelIntroduction
Diffusion Models have recently taken the world of generative AI by storm, producing incredibly realistic images and other complex data. While their success is most visible in computer vision, these powerful generative models are not limited to images. They hold immense potential for time series analysis, offering new approaches to forecasting, imputation, anomaly detection, and even synthetic data generation.
In this blog post, we’ll delve into the core concepts of Diffusion Models and then explore how they can be adapted and applied to the unique challenges of time series data.
What are Diffusion Models?
At their core, Diffusion Models are generative models that learn to reverse a gradual diffusion process. Imagine a clean image slowly being corrupted by noise over many steps. The Diffusion Model learns to reverse this process, step by step, to reconstruct the original clean image from pure noise.
This process typically involves two main phases:
- Forward Diffusion (Noising Process): A controlled amount of Gaussian noise is progressively added to the data over a series of timesteps, gradually transforming the original data into pure noise.
- Reverse Diffusion (Denoising Process): A neural network (often a U-Net architecture) is trained to predict and remove the noise at each step, effectively learning to reverse the forward process. By starting with random noise and iteratively applying the learned denoising steps, the model can generate new, realistic data samples.
Adapting Diffusion Models for Time Series
Applying Diffusion Models to time series data requires adapting their architecture and training process to account for the sequential and temporal dependencies inherent in time series. Key considerations include:
- Input Representation: Instead of 2D images, the model needs to handle 1D time series sequences. This might involve using 1D convolutional layers or recurrent neural networks (RNNs) within the denoising network.
- Conditional Generation: For tasks like forecasting, the model needs to be conditioned on past observations. This can be achieved by feeding the historical time series data as an additional input to the denoising network.
- Temporal Dependencies: The model must learn to respect the temporal order and dependencies within the data. Techniques like attention mechanisms or specialized temporal convolutions can help capture these relationships.
Applications in Time Series Analysis
Diffusion Models offer exciting possibilities across various time series tasks:
- Forecasting: By learning the underlying data distribution, Diffusion Models can generate multiple plausible future trajectories, providing a richer understanding of uncertainty compared to point forecasts.
- Anomaly Detection: Anomalies often deviate significantly from the learned data distribution. Diffusion Models can identify these deviations during the denoising process, flagging them as potential anomalies.
- Imputation: Missing values in time series can be treated as noise. The denoising process can then be used to fill in these gaps, generating realistic imputations.
- Synthetic Data Generation: For privacy-sensitive applications or when real data is scarce, Diffusion Models can generate high-fidelity synthetic time series data that preserves the statistical properties of the original data.
- Time Series Classification/Clustering: While not their primary use, the learned representations from the denoising process could potentially be used as features for downstream classification or clustering tasks.
Conclusion
Diffusion Models represent a powerful new frontier in generative AI, and their application to time series analysis is still an active area of research. By leveraging their ability to model complex data distributions and generate diverse samples, they offer innovative solutions to long-standing challenges in time series forecasting, anomaly detection, and synthetic data generation. As research progresses, we can expect to see even more sophisticated and impactful applications of Diffusion Models in the realm of time series.